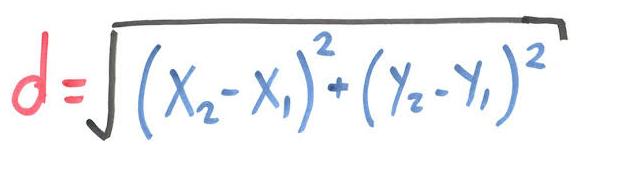PARÁBOLA
CONCEPTO
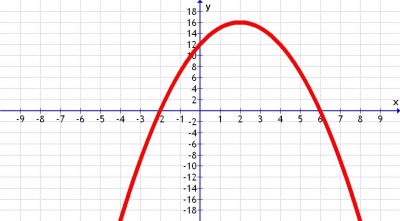 La Parábola es una figura geométrica que tiene forma de sección cónica, la cual resulta a partir de cortar en pequeños diferenciales un cono de punta redonda, se puede caracterizar también como el lugar geométrico de los puntos que equidistan de una recta (eje) y un punto fijo (foco) dados. La parábola aparece en muchas ramas de las ciencias aplicadas, debido a que las gráficas de ecuaciones cuadráticas son parábolas.
La Parábola es una figura geométrica que tiene forma de sección cónica, la cual resulta a partir de cortar en pequeños diferenciales un cono de punta redonda, se puede caracterizar también como el lugar geométrico de los puntos que equidistan de una recta (eje) y un punto fijo (foco) dados. La parábola aparece en muchas ramas de las ciencias aplicadas, debido a que las gráficas de ecuaciones cuadráticas son parábolas.
Click aquí para más información
TIPOS DE PARÁBOLA
Vertical
La ecuación de una parábola vertical corresponde a un polinomio de segundo grado:
y=a⋅x2+b⋅x+c
Donde a, b y c son constantes.

Horizontal
La parábola se define como el lugar geométrico de los puntos que equidistan de un punto fijo en el plano llamado foco y de una recta también fija en el plano llamada directriz. El punto medio entre el foco y la directriz se llama vértice. La distancia del vértice al foco o de del vértice a la directriz se le denota mediante la letra p. La siguiente figura muestra a una parábola que es paralela al eje x y que se abre a la izquierda:
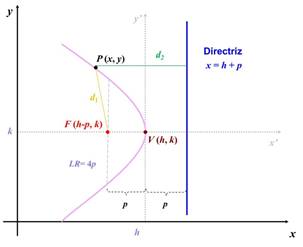
ELEMENTOS
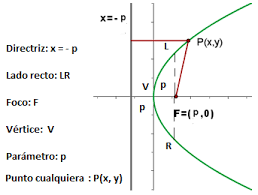
- Vertice
- Foco
- Parametro
- Directriz
- Lado Recto
Click para más información
FORMULARIO
FORMULARIO
| Tema |
Formula |
| Calcular la distancia entre dos puntos |
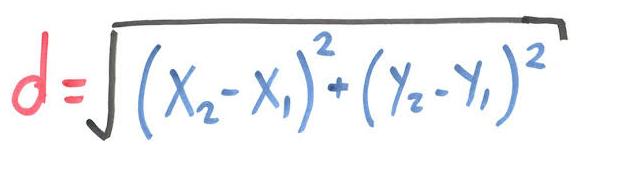
|
| Parábola se abre hacia la izquierda (sentido negativo) del eje de las abscisas “X” |
y^2= -4px |
| Ecuación de la directriz |
x-p=0 |
| Cuando la parábola se abre hacia arriba (sentido positivo) en el eje de las ordenadas “Y” |
x^2=4py |
| Ecuación de la directriz |
y+p=0 |
| Cuando la parábola se abre hacia abajo (sentido negativo) en el eje de las ordenadas “Y” |
x^2=-4py |
| Ecuación de la directriz |
y-p=0 |
GRACIAS POR VISITAR NUESTRO SITIO!!!
 La Parábola es una figura geométrica que tiene forma de sección cónica, la cual resulta a partir de cortar en pequeños diferenciales un cono de punta redonda, se puede caracterizar también como el lugar geométrico de los puntos que equidistan de una recta (eje) y un punto fijo (foco) dados. La parábola aparece en muchas ramas de las ciencias aplicadas, debido a que las gráficas de ecuaciones cuadráticas son parábolas.
La Parábola es una figura geométrica que tiene forma de sección cónica, la cual resulta a partir de cortar en pequeños diferenciales un cono de punta redonda, se puede caracterizar también como el lugar geométrico de los puntos que equidistan de una recta (eje) y un punto fijo (foco) dados. La parábola aparece en muchas ramas de las ciencias aplicadas, debido a que las gráficas de ecuaciones cuadráticas son parábolas.